HEP-like Simple Model¶
🎶 I’m the very Model of a simple HEP-like measurement… 🎶
HEP-like?¶
So what do we do as experimentalists in High Energy Physics? We have a gigantic detector that serves as a counting machine for physics. We smash particles and take pictures of the aftermath. Then we propose hypotheses for new physics that we want to test using this data. So we will have, at the very least:
signal
background (with some uncertainty)
some observations
This is probably the simplest model one could use in HistFactory… so let’s make it.
import pyhf
import json
model = pyhf.simplemodels.hepdata_like(signal_data=[5.0, 10.0],
bkg_data=[50.0, 60.0],
bkg_uncerts=[5.0, 12.0])
model
<pyhf.pdf.Model at 0x7f29d1f116d0>
What did we just make? This returns a pyhf.Model object. Let’s check out the specification.
print(json.dumps(model.spec, indent=2))
{
"channels": [
{
"name": "singlechannel",
"samples": [
{
"name": "signal",
"data": [
5.0,
10.0
],
"modifiers": [
{
"name": "mu",
"type": "normfactor",
"data": null
}
]
},
{
"name": "background",
"data": [
50.0,
60.0
],
"modifiers": [
{
"name": "uncorr_bkguncrt",
"type": "shapesys",
"data": [
5.0,
12.0
]
}
]
}
]
}
]
}
As we can see from the specification, we defined a single two-bin channel (‘singlechannel’) with two samples: a signal sample and a background sample. The signal sample has an unconstrained normalization factor \(\mu\), the signal strength, while the background sample carries an uncorrelated shape systematic controlled by parameters \(\gamma_{1}\) and \(\gamma_{2}\). The background uncertainty for the bins is \(10\%\) and \(20\%\) respectively.
These uncertainties are absolute (not relative!). We have 10% and 20% relative uncertainty for the bins in the background sample respectively.
(Note: we have a workspace defined with this simple model in data/2-bin_1-channel.json which we will look at later.)
Let’s explore the model a little bit.
print(f' channels: {model.config.channels}')
print(f' nbins: {model.config.channel_nbins}')
print(f' samples: {model.config.samples}')
print(f' modifiers: {model.config.modifiers}')
print(f'parameters: {model.config.parameters}')
print(f' nauxdata: {model.config.nauxdata}')
print(f' auxdata: {model.config.auxdata}')
channels: ['singlechannel']
nbins: {'singlechannel': 2}
samples: ['background', 'signal']
modifiers: [('mu', 'normfactor'), ('uncorr_bkguncrt', 'shapesys')]
parameters: ['mu', 'uncorr_bkguncrt']
nauxdata: 2
auxdata: [100.0, 25.0]
Auxiliary Data¶
Whoa, hold up! What’s with the auxiliary data? Remember from the previous chapter, we learned about the full likelihood
and the auxiliary data here is passed into a constraint function? There’s two things going on here:
the uncorrelated shapesys modifier is constrained by a Poisson
the auxiliary data is fully determined by the shapesys ‘data’ and the ‘background’ data
So if we were to explicitly write out the likelihood we were seeing symbolically, it would be:
where \(n = \{n_1, n_2\}\) for a 2-bin model (we’re being slightly fast and loose with our mathematical notation here), and similarly for \(s\), \(b\), and \(\gamma\).
The ‘shapesys’ is defined in the HistFactory paper… however, it can be a little hard to extract out the necessary information. We’ve provided a nice table of Modifiers and Constraints in the introduction of our pyhf documentation to use as reference.

Let’s look at the first row here which is our uncorrelated shape modifier. This is a multiplicative modifier denoted by \(\kappa\) per-bin (denoted by \(\gamma_b\)). Notice that the input for the constraint term requires \(\sigma_b\) which is the relative uncertainty of that modifier. This is Poisson-constrained by \(\sigma_b^{-2}\). Let’s quickly verify by hand to convince ourselves of what’s going on here:
import numpy as np
(np.array([5.0, 12.0]) / np.array([50.0, 60.0]))**-2
array([100., 25.])
model.config.auxdata
[100.0, 25.0]
Whew. Ok, I guess that makes sense.
Data and Parameters¶
What about the actual data for the model then?
model.expected_data()
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-6-f52b933f0780> in <module>
----> 1 model.expected_data()
TypeError: expected_data() missing 1 required positional argument: 'pars'
Hrmm, that didn’t work. It seems we need to specify the parameter values to get the data for the model at those parameter values. Well, we know the default for \(\mu=1\) and \(\gamma = 1\). Also recall that the uncorrelated shape allocates a parameter per bin, so our model has 3 parameters with 2 modifiers. So let’s just try that:
model.expected_data([1.0, 1.0, 1.0])
array([ 55., 70., 100., 25.])
This returns the data for the entire likelihood, the main model as well as the constraint (or auxiliary) model. We can also drop the auxdata to get the actual data.
model.expected_data([1.0, 1.0, 1.0], include_auxdata=False)
array([55., 70.])
Similarly, there are also methods separately for the actual data and the auxdata, both which take in all the parameters:
model.expected_actualdata([1.0, 1.0, 1.0])
array([55., 70.])
model.expected_auxdata([1.0, 1.0, 1.0])
array([100., 25.])
So how do we know what we should set the parameters to? The nice thing is that this is up to you! The model will come with some suggested defaults for parameters…
model.config.suggested_init()
[1.0, 1.0, 1.0]
… and their bounds…
model.config.suggested_bounds()
[(0, 10), (1e-10, 10.0), (1e-10, 10.0)]
… and if the parameter should be held constant in a fit or not …
model.config.suggested_fixed()
[False, False, False]
So armed with this knowledge, we could have also done
init_pars = model.config.suggested_init()
model.expected_actualdata(init_pars)
array([55., 70.])
To get the expected actual data from the model (signal + background). We could turn off the signal, corresponding with the normalization factor. We just need to know the index of the parameter:
model.config.poi_index
0
and then just change the parameter
bkg_pars = [*init_pars] # my clever way to "copy" the list by value
bkg_pars[model.config.poi_index] = 0
model.expected_actualdata(bkg_pars)
array([50., 60.])
Simple Inference¶
The core of statistical analysis is the statistical model. For inference, it’s viewed as a function of the parameters with the data fixed.
The value of the likelihood is a float. Let’s try it for both the background-only model as well as the signal+background model.
observations = [52.5, 65.] + model.config.auxdata
model.logpdf(
pars = bkg_pars,
data = observations
)
array([-11.92667279])
model.logpdf(
pars = init_pars,
data = observations
)
array([-11.90309416])
We’re not performing inference just yet. We’re simply computing the ‘logpdf’ of the model specified by the parameters \(\theta\) against the provided data. To perform a fit, we use the inference API via pyhf.infer.
To fit a model to data, we usually want to find the \(\hat{\theta}\) which refers to the “Maximum Likelihood Estimate”. This is often referred to mathematically by
Let’s perform a fit on this model to the provided observations we just made up.
pyhf.infer.mle.fit(
data = observations,
pdf = model
)
array([0.4999958 , 0.99999959, 1.0000017 ])
So what can we say? With nominal signal [5, 10] and nominal background = [50, 60], an observed count of [52.5, 65] suggests best fit values:
\(\hat{\mu} \approx 0.5\),
\(\hat{\gamma} \approx [1,1]\).
Simple Hypothesis Testing¶
Great, so we can fit. But that’s not usually the interesting part, since we cannot make any statements about this. What we prefer to do is perform a hypothesis test to either:
reject Standard Model hypothesis - a discovery fit
reject Beyond the Standard Model hypothesis - an exclusion fit
So we need to compute test statistics in order to evaluate the hypothesis. If we know the distribution of the test statistic under two different hypotheses, we can compute a CLs value. This is a modified pseudo-frequentist p-value.
with
This is done by splitting the model parameters up into two groups:
parameters of interest (POI - can have multiple!)
nuisance parameters (NP)
Recall that additionally, all parameters are either constrained or unconstrained. Parameters of interest happen to always be unconstrained parameters.
In the vast majority of cases, the test statistic is the profile likelihood ratio, or variations of it:
where
\(\hat{\hat{\theta}}\) is the best fitted value of the nuisance parameters (for fixed POIs)
\(\hat{\psi}\) and \(\hat{\theta}\) are the best fitted values in a global fit
So let’s run a hypothesis test for
null hypothesis (\(\mu = 1\)) - “SUSY is real”
alternate hypothesis (\(\mu = 0\)) - “Standard Model explains it all”
CLs_obs, CLs_exp = pyhf.infer.hypotest(
1.0, # null hypothesis
[52.5, 65.] + model.config.auxdata,
model,
return_expected_set = True
)
print(f' Observed CLs: {CLs_obs}')
for expected_value, n_sigma in zip(CLs_exp, np.arange(-2,3)):
print(f'Expected CLs({n_sigma:2d} σ): {expected_value}')
qmu test statistic used for fit configuration with POI bounded at zero.
Use the qmu_tilde test statistic (pyhf.infer.test_statistics.qmu_tilde) instead.
qmu test statistic used for fit configuration with POI bounded at zero.
Use the qmu_tilde test statistic (pyhf.infer.test_statistics.qmu_tilde) instead.
Observed CLs: 0.4856399484713726
Expected CLs(-2 σ): 0.08301671550449127
Expected CLs(-1 σ): 0.1825827716899532
Expected CLs( 0 σ): 0.3701533437480503
Expected CLs( 1 σ): 0.6434240650923724
Expected CLs( 2 σ): 0.8853038279362345
Nicely enough, pyhf is smart enough to let us know that, if for a model where \(\hat{\psi} < 0\), we’re not going to be able to catch it because our default bounds were bounding the parameter of interest from below at 0. For more information, see Equation 14 in [1007.1727].
model.config.suggested_bounds()[model.config.poi_index]
(0, 10)
We should heed the warning and switch our test statistic in this case to a variation of it \(q_\mu \to \tilde{q}_\mu\). We could also change the bounds from the default to allow \(\mu\) to float below zero. In this case, we’re just going to use a more appropriate test statistic as we know \(\hat{\mu} \geq 0\).
CLs_obs, CLs_exp = pyhf.infer.hypotest(
1.0, # null hypothesis
[52.5, 65.] + model.config.auxdata,
model,
return_expected_set = True,
qtilde=True,
)
print(f' Observed CLs: {CLs_obs}')
for expected_value, n_sigma in zip(CLs_exp, np.arange(-2,3)):
print(f'Expected CLs({n_sigma:2d} σ): {expected_value}')
Observed CLs: 0.4856399484713726
Expected CLs(-2 σ): 0.08301671550449127
Expected CLs(-1 σ): 0.1825827716899532
Expected CLs( 0 σ): 0.3701533437480503
Expected CLs( 1 σ): 0.6434240650923724
Expected CLs( 2 σ): 0.8853038279362345
Simple Upper Limit¶
To get upper limits, we just need to run multiple hypothesis tests for a lot of different null hypotheses of BSM with \(\mu \in [0, \ldots, 5.0]\) and then find the value of \(\mu\) for which the null hypothesis is rejected (a 95% \(\text{CL}_\text{s}\)).
poi_values = np.linspace(0.1, 5, 50)
results = [
pyhf.infer.hypotest(
poi_value,
observations,
model,
return_expected_set=True,
qtilde=True
)
for poi_value in poi_values
]
So this ran pretty fast. We can plot the “standard Brazil band” using the pyhf.contrib module (which needs pyhf[contrib]):
import pyhf.contrib.viz.brazil # not imported by default!
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
fig.set_size_inches(8, 8)
ax.set_title(u"Hypothesis Tests")
ax.set_xlabel(u"$\mu$")
ax.set_ylabel(u"$\mathrm{CL}_{s}$")
pyhf.contrib.viz.brazil.plot_results(ax, poi_values, results)
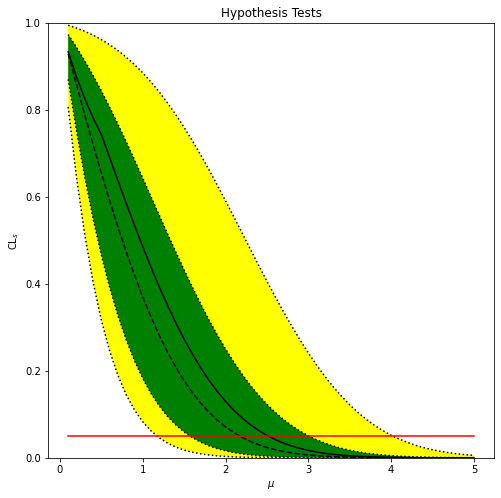
And then just calculate the upper limit by interpolating:
observed = np.asarray([h[0] for h in results]).ravel()
expected = np.asarray([h[1][2] for h in results]).ravel()
print(f'Upper limit (obs): μ = {np.interp(0.05, observed[::-1], poi_values[::-1])}')
print(f'Upper limit (exp): μ = {np.interp(0.05, expected[::-1], poi_values[::-1])}')
Upper limit (obs): μ = 2.5166992580821614
Upper limit (exp): μ = 2.1721797096236886
The upper limit here is the largest value of \(\mu\) for which the BSM hypothesis is not rejected.
