HistFactory

HistFactory#

pyhf stands for python-based HistFactory.

It’s a tool for statistical analysis of data in High Energy Physics.

In this chapter, we will cover

What HistFactory is in general
What pyhf is specifically (and what it is not)

Statistical Analysis#

We divide analyses into the type of fit being performed:

unbinned analysis (based on individual observed events)
binned analyses (based on aggregation of events)

Like HistFactory, pyhf does not work with unbinned analyses. These will not be covered in the tutorial.

So what uses HistFactory?

TRexFitter (ATLAS internal)
WSMaker (ATLAS internal)
HistFitter

Most everyone in SUSY and Exotics who performs an asymptotic fit as part of their analysis is likely using HistFactory!

Why Binned?#

Most likely, one performs a binned analysis if no functional form of the p.d.f. is known. Instead, you make approximations (re: educated guesses) as to this functional form through histograms.

What is a histogram? Fundamentally, a histogram is a tool to bookkeep arrays of numbers:

binning
counts
uncertainties

Beyond that, it contains helpful ingredients to make them more user-friendly for common operations (addition, division, etc…).

What are the ingredients?#

Once you have a model, you can perform inference such as

exclusion fit (upper limits)
discovery fit (lower limits)
measurement (two-sided intervals)
parameter scans
impact plots
pull plots
…

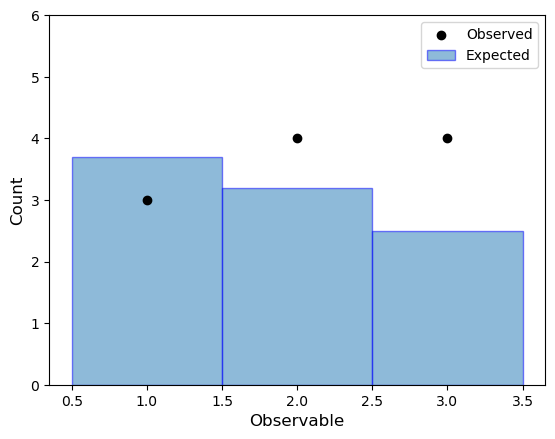
Let’s make up some samples and histograms to go along with it to understand what’s going on. Suppose we have an analysis with expected event rate \(\lambda\) and measurements \(n\). For this simple case, the overall probability of the full experiment is the joint probability of each bin:

\[ p(n|\lambda) = \prod_{\mathrm{bin}\ b} \mathrm{Pois}(n_b | \lambda_b) \]

A Poisson model is used as we are performing a counting experiment (counting the number of random events with an expected rate) in each bin of the observable.

import ipywidgets as widgets
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

bins = [1, 2, 3]
observed = [3, 4, 4]
expected_yields = [3.7, 3.2, 2.5]

fig, ax = plt.subplots()
ax.bar(bins, expected_yields, 1.0, label=r"Expected", edgecolor="blue", alpha=0.5)
ax.scatter(bins, [3, 4, 4], color="black", label="Observed")
ax.set_ylim(0, 6)
ax.legend()
ax.set_xlabel("Observable", fontsize=12)
ax.set_ylabel("Count", fontsize=12);

_images/5187f2a141b07b8cfe67e7c543255d17abdfced897b1a0e8441d404f616a65cc.png

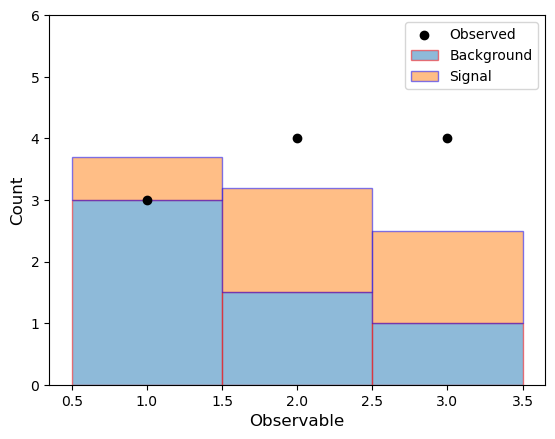
However, we don’t always often have just a single expected (simulation) sample, and \(\lambda\) is often the sum of multiple sample yields

\[ \lambda = \sum_{\mathrm{sample}\ s} \lambda_s \]

A typical case might be multiple (sub)dominant backgrounds or having a model where the observed events are described by a signal + background p.d.f. The model is then

\[ p(n|\lambda) = \prod_{\mathrm{bin}\ b} \mathrm{Pois}(n_b | \lambda_b) \qquad \lambda_b = \sum_{\mathrm{sample}\ s} \lambda_{bs} \]

bins = [1, 2, 3]
observed = [3, 4, 4]
background = [3.0, 1.5, 1.0]
signal = [0.7, 1.7, 1.5]

fig, ax = plt.subplots()
ax.bar(bins, background, 1.0, label=r"Background", edgecolor="red", alpha=0.5)
ax.bar(
    bins, signal, 1.0, label=r"Signal", edgecolor="blue", bottom=background, alpha=0.5
)
ax.scatter(bins, [3, 4, 4], color="black", label="Observed")
ax.set_ylim(0, 6)
ax.legend()
ax.set_xlabel("Observable", fontsize=12)
ax.set_ylabel("Count", fontsize=12);

_images/b17a66ceb84c0332851bf6dd1a9930dbe47085ffd2936f25fada3cdfad8a32c1.png

Already, you can see the p.d.f. for this simple case starts expanding to be a little bit more generic, and a little bit more flexible. Now we want to incorporate when the expected yields for signal and backgrounds depend on some parameters, perhaps how we applied calibrations to some objects, or how we configured our Monte-Carlo generators, etc.

Suppose we wanted a a normalization factor \(\mu_s\) scaling up (or down!) the sample. For example, if we want to parametrize the signal strength (without changing background). So \(\lambda\) becomes a function of \(\theta = \{\mu\}\) (a set of the parameters that determine the expected event rate), then our p.d.f. expands to be

\[ p(n|\lambda(\mu)) = \prod_{\mathrm{bin}\ b} \mathrm{Pois}(n_b | \lambda_b(\theta)) \qquad \lambda_b(\theta) = \sum_{\mathrm{sample}\ s} \lambda_{bs}(\theta) \]

where \(\mu_{\mathrm{background}} = 1\)

@widgets.interact(mu=(0, 5, 0.1))
def draw_plot(mu=1):
    bins = [1, 2, 3]
    observed = [3, 4, 4]
    background = [3.0, 1.5, 1.0]
    signal = [i * mu for i in [0.7, 1.7, 1.5]]

    print(f"signal: {signal}")
    print(f"background: {background}")
    print(f"observed: {observed}\n")

    fig, ax = plt.subplots()
    ax.bar(bins, background, 1.0, label=r"Background", edgecolor="red", alpha=0.5)
    ax.bar(
        bins,
        signal,
        1.0,
        label=r"Signal",
        edgecolor="blue",
        bottom=background,
        alpha=0.5,
    )
    ax.scatter(bins, [3, 4, 4], color="black", label="Observed")
    ax.set_ylim(0, 6)
    ax.legend()
    ax.set_xlabel("Observable", fontsize=12)
    ax.set_ylabel("Count", fontsize=12);

One final thing to finish our build up of a simplified HistFactory model is the concept of auxiliary measurements. Perhaps the background sample rate is modified by some normalization parameter, and we’ve made measurements of this parameter in a separate analysis (e.g. studies of the Jet Energy Scale). These prior experimental studies give a constraint that the parameter lies within a certain range.

For some parameters in a statistical model we don’t have prior experimental evidence for their values and must infer its values is the given analysis. These are unconstrained parameters (\(\eta\)) and enter into the main model as parameters of the event rate \(\lambda(\theta)\)

\[ p(n | \lambda(\theta)). \]

For many model parameters, their values in the model are constrained by a constraint term function, included in the model along with the the main model p.d.f, which describes auxiliary measurements/data (\(a\)) about the model parameter. These are constrained parameters (\(\chi\)) and enter into the model both in the constraint terms and as parameters of the event rate \(\lambda(\theta)\)

\[ p_\chi(a | \chi) \]

where \(\theta = \{\eta, \chi\}\). This constraining function model is chosen by the physics it represents, but in HistFactory most constraint terms are modeled as a Normal (Gaussian) or Poisson.

With the constraint terms the model expands to be

\[ p(n,a|\lambda(\theta)) = \prod_{\mathrm{bin}\ b} \mathrm{Pois}(n_b | \lambda_b(\theta)) \prod_{\mathrm{constraint}\ \chi} p_\chi(a_\chi | \chi) \qquad \lambda_b(\theta) = \sum_{\mathrm{sample}\ s} \lambda_{bs}(\theta) \]

where the expected event rate \(\lambda_b(\theta)\) is modified from its nominal value by a chosen interpolation function that smoothly interpolates between the up- and down-variations \((\pm1 \sigma)\) of the constraint term to provide an event rate modifier for any value of \(\chi\).

For this simple example, let’s consider a constraint term of a Normal distribution centered at \(\mu=0\) (“auxiliary measurement” \(a=0\)) with \(\sigma=1\) for constraining the normalization on the background where an up-variation (\(\mu_b = +1\)) scales by 1.3, and a down-variation (\(\mu_b = -1\)) scales by 0.8.

def normal_constraint(mu_b=0.0):
    # auxiliary measurement of 0
    # though note that for Normal observation and mean are symmetric under exchange
    return norm.pdf(0.0, loc=mu_b, scale=1.0)


# selected interpolation function
def interpolate(down, nom, up, alpha):
    if alpha >= 0:
        return (up - nom) * alpha + 1
    else:
        return 1 - (down - nom) * alpha


@widgets.interact(mu=(0, 5, 0.1), mu_b=(-1, 1, 0.1))
def draw_plot(mu=1, mu_b=0):
    bins = [1, 2, 3]
    observed = [3, 4, 4]
    background = [i * interpolate(0.8, 1.0, 1.3, mu_b) for i in [3.0, 1.5, 1.0]]
    signal = [i * mu for i in [0.7, 1.7, 1.5]]

    print(f"signal: {signal}")
    print(f"background: {background}")
    print(f"observed: {observed}")
    print(f"likelihood scaled by: {normal_constraint(mu_b)/normal_constraint(0.0)}\n")

    fig, ax = plt.subplots()
    ax.bar(bins, background, 1.0, label=r"Background", edgecolor="red", alpha=0.5)
    ax.bar(
        bins,
        signal,
        1.0,
        label=r"Signal",
        edgecolor="blue",
        bottom=background,
        alpha=0.5,
    )
    ax.scatter(bins, [3, 4, 4], color="black", label="Observed")
    ax.set_ylim(0, 6)
    ax.legend()
    ax.set_xlabel("Observable", fontsize=12)
    ax.set_ylabel("Count", fontsize=12);

However, notice that all along, we’ve been only discussing a single “channel” with 3 bins. The statistical analysis being studied might involve multiple channels corresponding to different analysis signal regions and control regions. Therefore, we compute the likelihood as

\[ p_\text{main} = p_\text{channel1} * p_\text{channel2} * p_\text{channel3} \cdots \]

We then expand out the likelihood definition further across channels

\[ p(n,a|\theta) = \underbrace{\prod_{\mathrm{channel}\ c}\prod_{\mathrm{bin}\ b} \mathrm{Pois}(n_{cb} | \lambda_{cb}(\theta))}_{\text{main}}\, \underbrace{\prod_{\mathrm{constraint}\ \chi} p_\chi(a_\chi | \chi)}_{\text{auxiliary}} \qquad \lambda_{cb}(\theta) = \sum_{\mathrm{sample}\ s} \lambda_{cbs}(\theta) \]

There are now two pieces of the model:

the main model, which consists of
- several channels (regions, histograms, etc), where
- each channel is a set of Poissons measuring the bin count for an expected value, where
- the expected value is the sum of various samples, where
- each samples expected value can be a function of parameters (or modifiers)
the constraint model, which consists of
- constraint terms on model parameters, where
- each constraint term describes auxiliary measurements

It should be clear by now that this is quite a lot of pieces to keep track of. This is where HistFactory comes in to play. Using HistFactory, we can

describe observed event rates and expected event rates
use well-defined modifiers to express parameterizations of the expected event rates
use well-defined interpolation mechanisms to derive expected event rates (if needed)
automatically handle auxiliary measurements / additional constraint terms

Note: if you’re curious about interpolation and interesting challenges, see the next chapter.

pyhf#

Up till 2018, HistFactory was only implemented using ROOT, RooStats, RooFit (+ minuit). pyhf provides two separate pieces:

a schema for serializing the HistFactory workspace in plain-text formats, such as JSON
a toolkit that interacts and manipulates the HistFactory workspaces

Why is this crucial? HistFactory in ROOT is a combination of loosely-linked XML+ROOT files

XML for structure
ROOT for storing data

These would then be processed through a hist2workspace command to get the ROOT Workspace that RooStats/RooFit use. As an example, let’s look at the provided multichannel HistFactory XML+ROOT as part of this tutorial:

!ls -lhR data/multichannel_histfactory

data/multichannel_histfactory:
total 8.0K
drwxr-xr-x 2 root root 4.0K Jul  4 10:21 config
drwxr-xr-x 2 root root 4.0K Jul  4 10:21 data

data/multichannel_histfactory/config:
total 20K
-rw-r--r-- 1 root root 6.4K Jul  4 10:21 HistFactorySchema.dtd
-rw-r--r-- 1 root root  906 Jul  4 10:21 example.xml
-rw-r--r-- 1 root root  974 Jul  4 10:21 example_control.xml
-rw-r--r-- 1 root root 1.1K Jul  4 10:21 example_signal.xml

data/multichannel_histfactory/data:
total 8.0K
-rw-r--r-- 1 root root 5.9K Jul  4 10:21 data.root

Here, we have two folders:

config which provides
- the XML HistFactory schema HistFactorySchema.dtd
- a top-level example.xml
- signal region and control region structures
data which provides the stored histograms in data.root

Let’s just look at the XML structure for now. What does the top-level look like?

!cat -n data/multichannel_histfactory/config/example.xml

<!--
//============================================================================
// Name        : example.xml
//============================================================================
-->

<!--
   Top-level configuration,  details for the example channel are in example_channel.xml.
   This is the input file to the executable.

   Note: Config.dtd needs to be accessible.  It can be found in ROOT release area.
   The file system path is relative to location of this XML file, not the executable.
-->

<!DOCTYPE Combination  SYSTEM 'HistFactorySchema.dtd'>

<Combination OutputFilePrefix="./results/example">
 <Input>./config/example_signal.xml</Input>
 <Input>./config/example_control.xml</Input>
 <Measurement Name="GaussExample" Lumi="1." LumiRelErr="0.1" ExportOnly="True">
   <POI>SigXsecOverSM</POI>
   <ParamSetting Const="True">Lumi</ParamSetting>
 </Measurement>
</Combination>

This top-level specifies:

15: the HistFactory XML schema
17: the workspace definition
18,19: channel definitions (links to other files)
20: a measurement GaussExample with specifications for luminosity, the parameter of interest, and setting lumi constant

What does the signal region look like?

!cat -n data/multichannel_histfactory/config/example_signal.xml

<!--
   Single channel configuration exampple.
   The top level configuration XML is example.xml

   NormalizedByTheory should be "True" (not "TRUE" or "true") for all non-data-driven backgrounds.

   If you comment or remove the <Data> tag then it will use the expected data.

   Histogram inputs should be in pb and in top-level xml the lumi should be in 1/pb
   (The important thing is that they match... fb and 1/fb is also ok)

   Note: Config.dtd needs to be accessible.  It can be found in ROOT release area.
   The file system path is relative to location of this XML file, not the executable.
-->

<!DOCTYPE Channel  SYSTEM 'HistFactorySchema.dtd'>

<Channel Name="channel1" InputFile="./data/data.root" >
 <Data HistoName="signal_data" HistoPath="" />
 <Sample Name="signal" HistoPath="" HistoName="signal_signal">
   <NormFactor Name="SigXsecOverSM" Val="1" Low="0." High="10."  />
 </Sample>
 <Sample Name="bkg" HistoPath="" NormalizeByTheory="True" HistoName="signal_bkg">
   <ShapeSys Name="uncorrshape_signal" HistoName="signal_bkgerr" ConstraintType="Poisson"/>
 </Sample>
</Channel>

This signal region specifies:

16: the HistFactory XML schema
18: the channel definition along with the path to the file for where the data for this channel is stored
19: where the expected event rate (data) for this channel is located
20, 23: sample definitions for signal and bkg with each sample expected event rate stored under HistoName in the corresponding ROOT file
21: a parameter SigXsecOverSM which is an unconstrained normalization factor
24: a parameter uncorrshape_signal which is a Poisson-constrained shape systematic, with the corresponding auxiliary data stored under HistoName in the corresponding ROOT file

As you can see, this works fine. It’s a little bulky, and a lot of loosely-tied information, but this fulls specifies the HistFactory model we’ve discussed so far.

In the next chapter, we’ll learn how to use pyhf to convert to the HistFactory JSON representation.